In a game, we often want to represent rotations: the main character’s head tilts left and right, the wheels of a vehicle rotate, characters follow curved paths through space.
There are many ways to represent a rotation mathematically, and each might have different benefits when we actually transform that math into code. Quaternions are one such way, and they are often favored because they are easy to interpolate; this means that given two rotations, we can easily transform one into the other in a smooth way without running into any issues.

For example, if the main character’s face is pointing down and to the right and his head is tilted sideways, it is possible to bring him back to facing straight ahead smoothly, using only the two quaternions corresponding to each orientation of the head.
This is why Quaternions are used in pretty much any 3D game engine out there.
You need four numbers to represent a quaternion. That might feel arbitrary, but it turns out that it’s related to the number of “different” 2D planes that can exist in 3D space.
It’s important to realize that rotations happen on 2D planes. In 3D, we usually think of rotations happening around an axis, like a wheel turning around its axle, but instead of thinking about the axle, we should think about the plane that the wheel lies on, perpendicular to the axle. Allow this old lady to demonstrate:

She is spinning wheel in the XZ plane, perpendicular to the Y axis. In addition, this is more like the 2D case where there is only one plane to rotate in. Considering rotations to happen around a third axis (perpendicular to the 2D plane) is technically incorrect, since we shouldn’t need to introduce another dimension to perform rotations.
In any case, this is what the code for a quaternion class might look like:
You can see that, aside from the scalar part, there are three numbers (x,y, and z), one per axis, or more properly one per plane perpendicular to each axis.
That’s all well and good, but we’re making a 4D game.
And we need to rotate things. So what about 4D rotations? It turns out there is a mathematical entity called a Rotor which can represent a rotation in any number of dimensions. As long as we think of rotations as happening on 2D planes instead of around 1D axes, everything works out fine. We just need to count the “different” 2D planes that can exist in 4D space. There are 6.
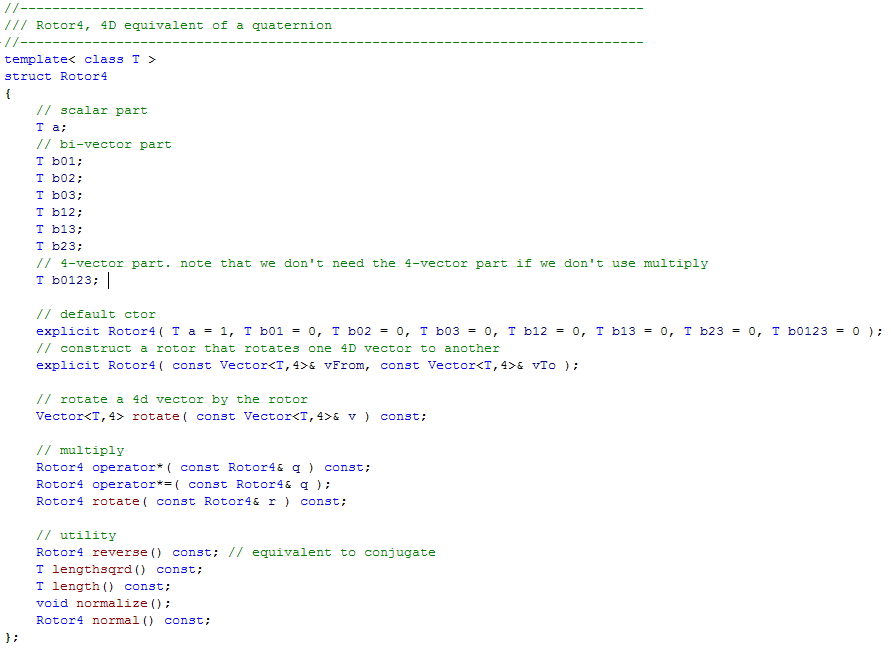
This is what the class definition for a 4D Rotor looks like:







Thanks for elaborating on this, I love to hear about development details, especially when it includes higher mathematics in R^n. Take this as positive feedback, I long for more ;). I still don’t understand why there are 4 ways to combine the three axis’ into different planes to rotate in, but I don’t expect you to spell it out for the dumb people (including me).
(In case anyone wants to chime in, here’s what I don’t get:
Isn’t the orientation of a plane already unambiguously defined by any one normal vector? In that case, we only have three linearly independent vectors to work with, so how does the fourth linearly independent vector come into being? You only mention three vectors “plus a scalar part” in your post. Am I misunderstanding everything again?)
You understood just fine. In 3D there are three vectors, which means three ways to rotate, and in addition to that we have the one scalar part.
and it will be absolutely worth it’s wait 😉
Thanks for the swift answer! If I visualize it as follows, would that be more or less correct?
You need three coordinates (x,y,z) to define the orientation of the plane to rotate around, and the scalar part would be something like the angle we rotate around.
@Max: It’s kind of like that, yes.
(sorry for the double post, I hit submit a bit too fast)
consequently, similar to how we need two coordinates (angle, scalar) when working with polar coordinates in R², we need (angle, angle, scalar) to achieve the same in R³, right?
Right, what you’re talking about is termed spherical coordinates. Cylindrical coordinates are another possible way of describing positions in 3D space, which takes polar and just specifies the z-coordinate. However, polar, spherical and cylindrical coordinates are all ways of defining position. Rotations in 2D space only require one scalar angle quantity, since there’s really only one way to rotate anything (two, if you count negative rotations in the opposite direction, but those can be included without loss of generality).
In 3D space, we need four quantities. Like you talked about in the first half of your double post, these can be defined based on the components of the vector defining the plane within which we rotate and the angle by which we rotate. That formulation of 3D rotation is known as the Euler vector/angle (there are several ways to specify 3D rotations, and more than one associated with the almighty Euler). However, quaternions take this construct further into the abstract world. The hyperimaginary components, at least in the convention used for quaternion representation of spacecraft rotations, uses the cosine of the angle of rotation (divided by two for convenience) as the real part and the sine of the angle (again divided by two) multiplied by each of the three components of the Euler vector to define the hyperimaginary parts of the quaternion. 3D rotations can be written in as many ways as there are people with the time to decide their way is the best, but so far quaternions are one of the most popular because they make the math more convenient later on.
Probably much too late to be helpful to anyone, but seeing that anyone still as obsessed with this game as I am must be pretty patient, maybe not.
I guess you know Clifford algebras, don’t you?
They make like so much easier.
(http://en.wikipedia.org/wiki/Geometric_algebra)
@ Omer: That’s right, I used Geometric Algebra. If you look at the Rotor class, you can see it has a 2-vector part and a 4-vector part.
Is it strange that I got a little glee out of understanding this?
I really wanted to understand this, but i cant… but theres no problem, ill read this again and again until i get it… 🙂 thanks for trying to make it easy to understand.
Interesting code snippetand mathematical discourse (working on multidimensional vectors has become somewhat of a hobby for me of late). I still implore you open up the source code so we can speed up development and improve features. The profit potential for you is still there, a suitably chosen license can be used as leverage for selling extra rights to commercial game studios. I have done some work on a game logic engine that might help you to concentrate on the geometry aspects and less on the more mundane work.
http://science.howstuffworks.com/science-vs-myth/everyday-myths/see-the-fourth-dimension.htm
Is there any reason you don’t just use a pair of quaternions?
@William I just like the idea that rotors generalize to any number of dimensions.
In your example quaternion code, x y and z are hyperimaginary, not just normal imaginary. Which is totally unnecessarily pedantic, except for the fact that the hyper-imagination is so much cooler. Because hyper.
That made me happy
hyper-happy