The shape at the end of the trailer is called a 120-cell (or Polydodecahedron, or Hecatonicosachoron, which sounds cooler, but a bit too hard to pronounce). It is actually modified a bit, but first let me explain some basics.
You see, a 3D object has a 2D surface, whereas a 4D object has a 3D surface (an nD object has an (n-1)D surface). So while a dodecahedron has 12 faces which are pentagons, a 120-cell has 120 “faces” which are dodecahedra (called cells, since they are 3D).
The 120-cell is a Convex Regular Polychoron, the 4D analogs of the 3D Platonic Solids (Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron). All the faces of a 3D platonic solid are the same 2D regular polygon, while all the cells of a “4D platonic solid” are the same 3D platonic solid! It’s basically building shapes out of the the most symmetrical elements each time.
Interestingly, there are infinitely many regular 2D polygons (just divide the circle equally into n sides: triangle, square, pentagon, etc…), 5 regular 3D convex polyhedra, 6 regular 4D convex polychora, but in 5D or more there are only 3 types! It appears that building shapes this way gets more and more complex until it is no longer possible, save for a few very generalizable cases (the hypercube, for example).
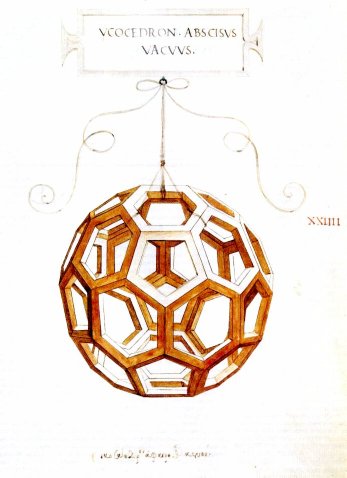
But what you see in the game is not quite a 120-cell, it is actually a 120-cell with a hole inside each cell. My friend Vi Hart [Youtube Channel] came up with the idea to do this, inspired by drawings by Leonardo Da-Vinci.
In the drawings, a hole has been cut inside each 2D face, or rather only the edges are visible. In the game a hole has been cut inside each 3D cell (each cell is hollow), or rather only the faces are visible.
The way this is implemented in the game engine is using our 4D Mesh Structure (a 3D mesh is made out of triangles, a 4D mesh is made out of tetrahedra).
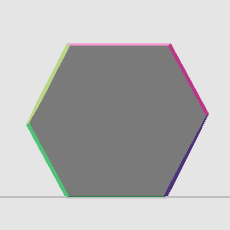
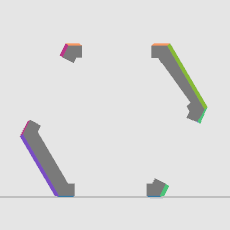
What you see is a 3D slice of a 4D object. While the 4D object is static, the 3D object you see transforms as the slice changes, similar to what you see in a moving slice produced by an MRI machine, but in one higher dimension (The image on the right is an MRI slicing though a banana flower).
The reason the number of faces changes is that depending on which slice you take, you might go though a different number of cells (each cell you slice will produce a face). If you slice the 4D object near its tip, you will get a small 3D object. If you slice the 4D object near the center, you will get a larger object. This is similar to slicing a 3D sphere with a 2D plane. Use the following sliders to slice through a dodecahedron, and its “Davinci’d” version. (Note that in the game we are rotating the 3D slice whereas here I am letting you move a 2D slice up and down, but the morphing effect is the same).










The detail that’s going into this game is incredible. It’s a shame that for most people who play it, a lot of that detail will be invisible.
Yeah! That’s ok, the beauty is visible in the details, even if you don’t understand.
“So while a dodecahedron has 12 faces which are pentagons, a 120-cell has 120 ‘faces’ which are dodecahedra (called cells, since they are 3D).”
So why, on the picture, does the 3D shape have more than 12 faces ? And why does the number of faces change when you move along the 4th dimension ?
Just updated the post.
I was describing the game to a friend the other day and I have a few questions now about points I couldn’t aptly determine!
-Does the player have the option to rotate the 3D hyperplane into 4-space both “clockwise” and “counterclockwise”? Or “clockwise” twice in a row (such that you’d end up back in an apparent mirror image of the original 3D space)?
-To what extent can the player control the speed of the rotation, since some segments in the trailer show a bit of slow-down action?
You press the button once to rotate clockwise, then again to rotate back (=counterclockwise).
Holding down the button slows down the speed of rotation.
This is tantalising marc, keep it up! 🙂
So what would this look like if the cells themselves were like Da-Vinci’s edge-only solids? (i.e. the cells weren’t just hollow, their faces were empty, too). Is that even a meaningful question?
Or perhaps it would look identical, just the smallest dodecahedron cell (at the beginning) would be sans-faces, too?
You would get lots of floating shapes, since slicing edges will give points.
No, no sliced edges – just open-faced dodecahedrons. On further reflection I think you might mean slicing cells would yield floating edges.
Kind of like how slicing Da’Vinci’s solids would result in odd partial-pieces of polygons.
I’m then unclear why the dodecahedron at the beginning of the gif has recessed sides the way it does.
(Really looking forward to this, in case it wasn’t clear!)
Yeah, slicing Da-Vinci solids would result in lots of tiny separate polygons, and so the 4d version would be much the same except they would be polyhedra instead of polygons.
It has recessed side because it is hollow! You are seeing a slice at an angle that reveals that fact.
That .gif is so beautiful 😀 Can’t wait to play it when it’s done!
You can buy a 3D projection of a 120-cell showing all 120 faces from http://www.bathsheba.com/math/120cell/
Thankyou Marc for your amazing work! I hope the game will be ready soon.
I’m a math teacher and, everytime I explain my students 3D geometry, I show them the trailer. First time I did this was in 2010, to boys in 1st class. Now they are in 5th class… and the game is still in development 🙂
Amazing!
Will the game feature all the 6 regular 4D polyhedra or just this one?
Seems likely.
There’s a nice set of very visual lectures about higher dimensional geometry produced a few years back called “Dimensions”. Amongst other things, it shows how 3D solids can be projected into 2D by pushing them through S2, and proceeds to do the same for 4D solids, projecting them into 3D via S3. Some of the visualizations are very pretty. http://www.dimensions-math.org/
Would it be possible to release a video where we see the actual 4D objects
I do realise it would be extremly messy as showing a 4D object on a 2D surface would make most details stack above each other but still, would it be possible? Or there is some tech limitation. I know computer use some specific formula to render 2D or 3D on screen, I guess there’s no formula to render 4D on 2D ^^’…
It’s possible and messy, yeah! If you look on Wikipedia there’s a bunch of that: https://en.wikipedia.org/wiki/120-cell for example