
“The laws of the model’s nature have to be logically and mathematically consistent with one another, but not with physics.” -J.C.R. Licklider (see previous post)
What makes a logically and mathematically consistent system? It seems to me that every system has a boundary within which it is consistent, and outside the boundary it starts to break down. How do we define this boundary?
The process of describing reality using mathematics is not perfect. First, an abstraction layer needs to be selected. That means we have to decide how detailed a model will be. If the model is too detailed, it will take too much “computation” to predict anything. If the model is too coarse, it might not predict enough effects.
For example, we can simulate the motion of an object by simulating every atom inside of it, but that may be unnecessary, and if the object does not deform very much at the scale we care about we can approximate it by a rigid body, which gives a simpler model that could work very well for our case. But if too much force is applied the object would start to deform or fracture, and then the model breaks down, and might give nonsense results.
In physics, we may know if the assumptions we make are reasonable or not. If we know for sure that in the situation we want to model not enough force will be applied to the object and thus it will never break, then it does not matter that the model does not handle this case.
In games, we create a set or rules for the game that often approximates reality to some level. So already we have chosen an abstraction layer. But we may not know what the consistency boundary of that model is, i.e. find out the places where the approximations we made result in nonsense situations. We may need to discover the shape of this boundary by playing the game itself. Like in physics, we can adjust the rules of the system to increase or decrease the consistent area, but unlike physics we are not bound by having to approximate reality.
For example, imagine a game where a character moves in a 2D grid and the player can place an arrow on a square to redirect it. This model assumes that the character can only move horizontally of vertically within the grid, and so far this is consistent. But what happens if you let players place two arrows on top of each other? If the effects are additive, suddenly diagonal movement needs to be considered, but the model so far has not taken this case into account. This is the edge of the consistency boundary. At this point we need to either disallow the case of diagonal movement and potentially make the game less rich and interesting, or allow the case and grow the consistency boundary, but this may be hard to design as new rules need to be created, and problematic areas may still exist, just further away.
Sometimes, problematic cases can be avoided by level design instead of system design. You can design the levels of the game such that this situation can never occur (ex: what if no more that one arrow is ever given to the player?).
This process of stripping away problematic cases is a lot of what game design is, at least in my experience. There are ways in which it can be done elegantly and inelegantly. Inelegant ways often leave the problematic cases apparent. The player can see the parts that have been cut of, or worse, they are forced to understand details about it. Presumably the system is the interesting part, not its boundary (though games that explicitly explore this idea could be designed and may be interesting).
In the aesthetics of game design, I feel like a game that is very consistent is more beautiful than one that is not.
The thing I talked about before is that in games the goal is not to simulate reality, so we have an extra tool in our hands: generalization. For example if SimCity is a model of a city, then adding Godzilla to it is a generalization. Or taking an FPS (which is a simulation of a person walking in an environment) and adding portals.
This creates additional problems because while we are fairly certain that reality is consistent, we do not know about other, generalized, realities. (If the first part is like physics, this part is a bit like inventing new mathematics).
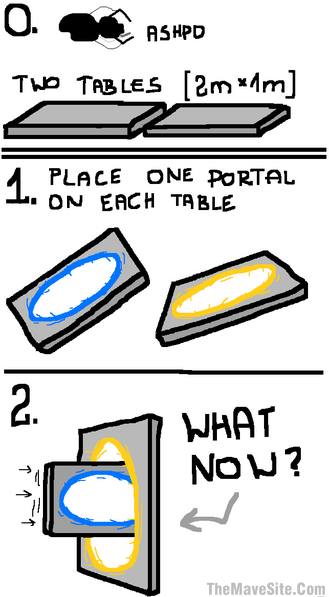
So for example, it appears to me that Portals are not very consistent. A lot of issues appear pretty quickly, as seen in these drawings I found online:
It might be interesting to try to design Portal in a way that would allow for more consistency, and gets closer to handling cases such as these. I am not sure this is possible.
Sometimes consistency can be improved by fixing things near the boundary, and sometimes the whole system needs to be rethought from first principles.

Another example: What happens in Fez when you get projected behind an object? This is an inconsistent situation that needs to be resolved with additional rules from the designers of the game. It comes from the many-to-one nature of projection.
Miegakure was surprisingly consistent. You can take almost any concept and generalize it to 4D. There are very few consistency problems in gameplay, mainly related to the rules of pushing blocks, which would happen in any number of dimensions. So because there is so much consistency in terms of the 4D generalization, the problem has been finding a good level of abstraction, especially graphically. In some way there are two types of consistency boundaries. The consistency problems that come from abstracting, and the consistency problems that come from exploring. The abstraction consistency boundary seems contained within the generalization consistency boundary.
Sometimes I want to make things clearer or more beautiful at the expense of correctness. Or rendering 4D properly is sometimes too slow (just like 3D graphics are just an approximation of reality!). For example I spent a long time on the extruded 3D trees and it was well worth it. The goal was to get a more detailed level of abstraction of what a four-dimensional universe would look like. But I will talk about it in a later post.







Thanks for the post. Do not understand consistency problem with Fez. The projection is correct and consistent – player sees external boundary of a wall. The slide describes problem that it’s not obvious to the player where exactly Gomez got projected. So they decided to draw silhouette and dampen the music. Do you want game to show the exact slice where Gomez is located ? if so it’s the problem with the view, not game system.
Gomez is not on a slice, his position along the projected axis (let’s call it the z-axis) changes as he walks from tile to tile. I guess you could hide any tile that is in front of his current z position, but then it would not be a projection anymore, and not be consistent with the rest of the game, hence the inconsistency.
I use following logic: Gomez does not exist when he gets projected behind a wall. One way to resolve it is to undo faulty rotation(it’s kind of a failure state). But it would cause player frustration and lack of understanding. So showing silhouette behind a wall helps player to fix faulty rotation by moving character to correct location. The projection system remains consistent and is forgiving to player mistakes.
Ok, if you mean it in that sense, I would say just the existence of a faulty state is an inconsistency.
It’s not even that the state is “faulty”. It’s just that, when behind a wall, Gomez ceases to exist, in the same way that many objects cease to exist in various projections. But since Gomez is the player-character, we don’t want to follow through with that. To be “consistent”, you’d simply be unable to do anything until you rotate away from that projection. That’d be frustrating or boring. So Fez makes a purposeful exception in order to let the gameplay continue to flow.
That is not what I am talking about. The very existence of an exception shows there is an inconsistency to fix.
I think it would be consistent to have Gomez not exist when he is completely behind something, but what about when he is partially behind something? I think this is where you run into the inconsistency problems Marc is referring to. He can’t only half exist.
For the record, yesterday I’ve seen somebody explaining the second Portal image:
1) The rod would keep accelerating downwards thanks to gravity (which still applies). It’d keep accelerating forever (well, within the limitations normal physics allow it to).
2) Portals are not stable enough to persist if they’re moved (it seems some puzzles rely on this), so the portals would vanish as soon as the surface is moved, and the rod would most likely snap since it’s forcefully cut where the portals were.
3) The rod would probably break instantaneously, preventing it from expanding to infinite.
#2 has a catch: Earth is constantly moving around, so obviously the movement rule is relative to the current environment. Maybe it’s the change in speed that causes the issue, which would bring back the problem (in different scenarios). Then again, if portals are that unstable, it’s likely there are other impossible situations where they’d just vanish as well.
The left image probably can be explained with the same logic I just mentioned: portals are most likely unstable enough that they’d vanish if they touched each other. The chunk of table that had already entered the orange portal would get cut much like the rod before.
The “portals are unstable” logic seems like a escapegoat but there are situations exactly like that in real world physics too =P Some things simply can’t happen at all.
All I am saying is that if you have to define special rules like “portals are unstable” then it is inconsistent at that point.
I’ve mostly been on track with you (and I’m aware this is old, but forgive me), but this response here is total bullshit. The entire conception and definition of a ‘portal’ is a collection of ‘special rules’. As long as those rules don’t ever clash with each other, you can have as many as you like and call it consistent. Adding a ‘stability clause’ to the rules, and defining that stability as violated when moved, is not inconsistent at all.
Likewise, in physics, we have lots of ‘special rules’. You can call quantum physics ugly, and plenty of people do, but it certainly isn’t inconsistent.
By the way, I’m a huge fan of your work and am dying to try your game. I have some ideas I’d love to talk over with you as well, if you were available.
I think I agree with you, and you are simply misunderstanding me.
I agree that portals are pretty much a collection of special rules, which is why they are quickly going to have what I define as consistency problems. But you can say, assume these special rules, what effects can I get out of them? If you need one more special rule for a particular effect, then you are at the consistency boundary (the system is inconsistent for this effect) and you need to make the decision of whether or not to add the rule. Adding the rule may make the system consistent again. The ugliness comes from the number of special rules, and from crudely snipping away cases like moving portals.
You can email me if you want. My contact info is on my home page.
In the post I say things like “Miegakure was surprisingly consistent,” by which I mean: it had a surprisingly large consistent space: very few rules got me very far until I reached the consistency boundary.
“The laws of the model’s nature have to be logically and mathematically consistent with one another, but not with physics.” This quote is interesting because video games (or any computation), must be a logically consistent to work (though I’m not sure where computability of a program of a model fits in with consistency of the model).
Say we have a designer who wants to show some aspect of reality in their game. They create a model that approximates or just is (in the case of a mathematical concept) what they want to show. In this case the player may feel an inconsistency if they either do not understand the concept or they reach the boundary between the simulation (if it is)
Any rule that designer adds on top of their model is to handle a case that had (a) an undesirable result or (b) was actually inconsistent when they started working with code, since they could not code the inconsistency, or would have encountered it while trying to build the model.
All of this is actually to try and parse out the fact that the post refers to multiple different kinds of inconsistency (which caused me some confusion):
-the mathematical and logical kind which may exist in the designers or players model
-the consistency between the model the player/designer has in their head and the one implemented in the game
-the one implemented in the game and how something similar behaves in reality
Anyway and good read, and it got me thinking about these inconsistencies which is interesting.
This is essentially a standard problem in mathematical logic. Broadly a system is inconsistent if you can prove two mutually exclusive results in it. Quite often it’s impossible to prove a system is consistent – the best we can do is say that if system A is consistent, then system B, which is an extension of A is also consistent. If we assume that normal 3D geometry is consistent then we have to see if 3D geometry plus portals is also consistent. The examples given don’t show that portals are inconsistent; we would have to prove that there is no model which allows them. In the case of the welded rod, I would argue that the two portals are co-incident. Therefore topologically the rod forms a circle, which just appears straight because space is bent by the portals. It will continue to accelerate in the first example, just as any other object does (free energy!).
In the second example, the rod itself will hold up the portal, unless the object the portal is in is too heavy, in which case the rod will buckle.
The third example is the interesting one. If you continuously move the portal exit to its new position then you will bend the rod, as described in the second example. If you use the portal gun to move the portal then you have an inconsistency, as there is a time when the portal entrance exists but not the exit – a hole with only one end. This can be resolved if you assume that the portal entrance is merely potential until the exit is created. In that case, the rod cannot pass through it. At this point, the straight rod in warped space becomes a warped rod in flat space – either the weld breaks or the rod buckles. Therefore it is only possible to move the portal exit, either discretely or continuously, if you can supply sufficient energy to allow the rod to deform.
Similarly, although far more confusingly, as you pass one portal through another, the material of the table will eventually try to intersect with itself. Any further motion is stopped unless you can push hard enough to crush the wood. I haven’t worked through the logic completely, but I also suspect that you will find that object will bounce off the line of intersection of the two portals as any attempt to pass through it would entail an infinite number of copies of the object in the same space. That way lies singularity and the breakdown even of portal physics
Ultimately, all of the Portal problems come down to how do you supply sufficient energy to warp space that severely and how do the portals supply the extra potential energy given when you enter a lower portal and exit a higher one. The portal gun must have an impressive power pack
Wow, that’s an impressive endeavour to make portal physics consistent! I like your solutions to the problems, which may very well be reasonable within the lack of our current physical knowledge of warped space, and your mathematical and physical musings.
I think the biggest video game inconsistency, though, is how can Spyro glide at such a low angle, with such tiny wigs relative to his body? All the other dragons have huge wings that actually look like they might be able to fly, but Spyro’s got less than a wingsuit of material there. Just not logical…
I’ve been a bit foggy about what part of this game you can view for mathematical consistency, I apologize if this is off topic or has been explained. For example, I was looking at the level where you move the cube out of the large temple: I understand the concept of moving between slices of various 3d worlds, but in the video each 3d world looked completely separate from one an other. In other words, you can make one a completely barren snowy world, and an other has a large temple in it, so I don’t see how there is any mathematical connection between the two? Couldn’t you just put anything you wanted in any of the worlds? What happened to the idea of seeing various sides of a 4d object? I am having difficulty interpretting any of the 3d environments as part of a 4d object.. They all seem isolated… Is there any way you can point out to me in a specific example how they are part of one object? I understand the general concept, however, I think. But I’m not understanding how math is needed.
Hi James, I come a bit late, but in case you didn’t find the answer to your question yet, here’s the link to a video that explains how it’s all (couinter-intuitively) consistant: https://www.youtube.com/watch?v=9yW–eQaA2I
Looking forward to that post about trees
Excellent series of essays, marc, this could easily find place in a volume on game design.