In a game, we often want to represent rotations: the main character’s head tilts left and right, the wheels of a vehicle rotate, characters follow curved paths through space.
There are many ways to represent a rotation mathematically, and each might have different benefits when we actually transform that math into code. Quaternions are one such way, and they are often favored because they are easy to interpolate; this means that given two rotations, we can easily transform one into the other in a smooth way without running into any issues.

For example, if the main character’s face is pointing down and to the right and his head is tilted sideways, it is possible to bring him back to facing straight ahead smoothly, using only the two quaternions corresponding to each orientation of the head.
This is why Quaternions are used in pretty much any 3D game engine out there.
You need four numbers to represent a quaternion. That might feel arbitrary, but it turns out that it’s related to the number of “different” 2D planes that can exist in 3D space.
It’s important to realize that rotations happen on 2D planes. In 3D, we usually think of rotations happening around an axis, like a wheel turning around its axle, but instead of thinking about the axle, we should think about the plane that the wheel lies on, perpendicular to the axle. Allow this old lady to demonstrate:

She is spinning wheel in the XZ plane, perpendicular to the Y axis. In addition, this is more like the 2D case where there is only one plane to rotate in. Considering rotations to happen around a third axis (perpendicular to the 2D plane) is technically incorrect, since we shouldn’t need to introduce another dimension to perform rotations.
In any case, this is what the code for a quaternion class might look like:
You can see that, aside from the scalar part, there are three numbers (x,y, and z), one per axis, or more properly one per plane perpendicular to each axis.
That’s all well and good, but we’re making a 4D game.
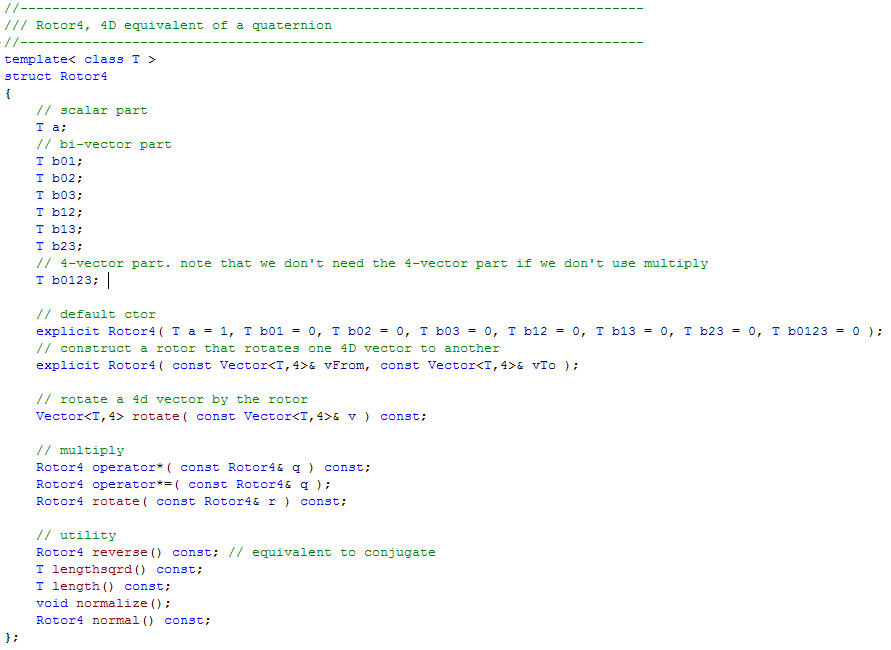
And we need to rotate things. So what about 4D rotations? It turns out there is a mathematical entity called a Rotor which can represent a rotation in any number of dimensions. As long as we think of rotations as happening on 2D planes instead of around 1D axes, everything works out fine. We just need to count the “different” 2D planes that can exist in 4D space. There are 6.
This is what the class definition for a 4D Rotor looks like: