“The laws of the model’s nature have to be logically and mathematically consistent with one another, but not with physics.” -J.C.R. Licklider (see previous post)
What makes a logically and mathematically consistent system? It seems to me that every system has a boundary within which it is consistent, and outside the boundary it starts to break down. How do we define this boundary?
The process of describing reality using mathematics is not perfect. First, an abstraction layer needs to be selected. That means we have to decide how detailed a model will be. If the model is too detailed, it will take too much “computation” to predict anything. If the model is too coarse, it might not predict enough effects.
For example, we can simulate the motion of an object by simulating every atom inside of it, but that may be unnecessary, and if the object does not deform very much at the scale we care about we can approximate it by a rigid body, which gives a simpler model that could work very well for our case. But if too much force is applied the object would start to deform or fracture, and then the model breaks down, and might give nonsense results.
In physics, we may know if the assumptions we make are reasonable or not. If we know for sure that in the situation we want to model not enough force will be applied to the object and thus it will never break, then it does not matter that the model does not handle this case.
In games, we create a set or rules for the game that often approximates reality to some level. So already we have chosen an abstraction layer. But we may not know what the consistency boundary of that model is, i.e. find out the places where the approximations we made result in nonsense situations. We may need to discover the shape of this boundary by playing the game itself. Like in physics, we can adjust the rules of the system to increase or decrease the consistent area, but unlike physics we are not bound by having to approximate reality.
For example, imagine a game where a character moves in a 2D grid and the player can place an arrow on a square to redirect it. This model assumes that the character can only move horizontally of vertically within the grid, and so far this is consistent. But what happens if you let players place two arrows on top of each other? If the effects are additive, suddenly diagonal movement needs to be considered, but the model so far has not taken this case into account. This is the edge of the consistency boundary. At this point we need to either disallow the case of diagonal movement and potentially make the game less rich and interesting, or allow the case and grow the consistency boundary, but this may be hard to design as new rules need to be created, and problematic areas may still exist, just further away.
Sometimes, problematic cases can be avoided by level design instead of system design. You can design the levels of the game such that this situation can never occur (ex: what if no more that one arrow is ever given to the player?).
This process of stripping away problematic cases is a lot of what game design is, at least in my experience. There are ways in which it can be done elegantly and inelegantly. Inelegant ways often leave the problematic cases apparent. The player can see the parts that have been cut of, or worse, they are forced to understand details about it. Presumably the system is the interesting part, not its boundary (though games that explicitly explore this idea could be designed and may be interesting).
In the aesthetics of game design, I feel like a game that is very consistent is more beautiful than one that is not.
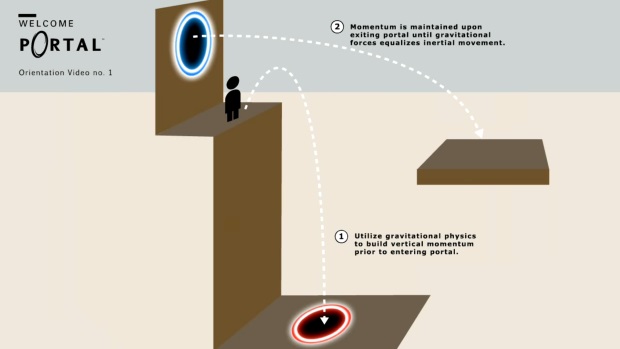
The thing I talked about before is that in games the goal is not to simulate reality, so we have an extra tool in our hands: generalization. For example if SimCity is a model of a city, then adding Godzilla to it is a generalization. Or taking an FPS (which is a simulation of a person walking in an environment) and adding portals.
This creates additional problems because while we are fairly certain that reality is consistent, we do not know about other, generalized, realities. (If the first part is like physics, this part is a bit like inventing new mathematics).
So for example, it appears to me that Portals are not very consistent. A lot of issues appear pretty quickly, as seen in these drawings I found online:
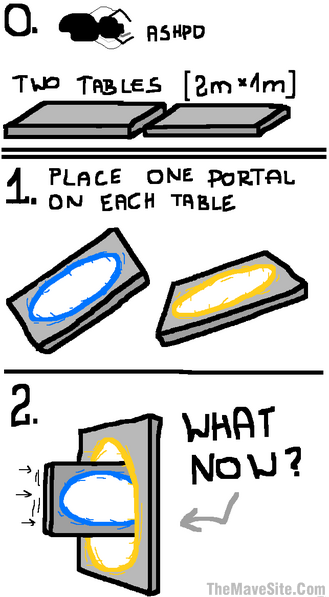

It might be interesting to try to design Portal in a way that would allow for more consistency, and gets closer to handling cases such as these. I am not sure this is possible.
Sometimes consistency can be improved by fixing things near the boundary, and sometimes the whole system needs to be rethought from first principles.

Another example: What happens in Fez when you get projected behind an object? This is an inconsistent situation that needs to be resolved with additional rules from the designers of the game. It comes from the many-to-one nature of projection.
Miegakure was surprisingly consistent. You can take almost any concept and generalize it to 4D. There are very few consistency problems in gameplay, mainly related to the rules of pushing blocks, which would happen in any number of dimensions. So because there is so much consistency in terms of the 4D generalization, the problem has been finding a good level of abstraction, especially graphically. In some way there are two types of consistency boundaries. The consistency problems that come from abstracting, and the consistency problems that come from exploring. The abstraction consistency boundary seems contained within the generalization consistency boundary.
Sometimes I want to make things clearer or more beautiful at the expense of correctness. Or rendering 4D properly is sometimes too slow (just like 3D graphics are just an approximation of reality!). For example I spent a long time on the extruded 3D trees and it was well worth it. The goal was to get a more detailed level of abstraction of what a four-dimensional universe would look like. But I will talk about it in a later post.