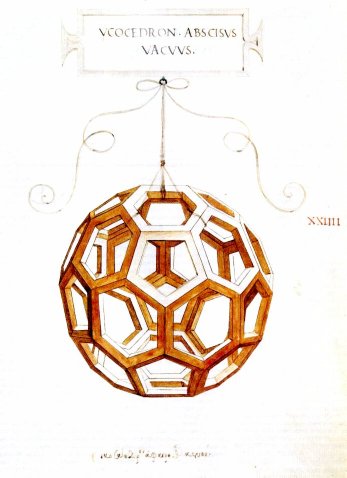
A question that people ask me once in while is: Do you think your conception of reality has changed from making this game?
I find that one of the things that excite me the most about Miegakure is that because it takes concepts familiar in three dimensions and generalizes them to four dimensions (or even n dimensions) it distills these concepts to a more fundamental core. There is something more truthful about a concept that has been distilled to a simpler form, but it also helps us understand the concept better.
A good example is rotation. A rotation is fundamentally a 2D thing; you need two dimensions to define a plane of rotation. We are so used to thinking about rotations in 3D that we think about the axis of rotation, but this doesn’t generalize to nD: the 2D plane that is perpendicular to that axis is what is important. The focus on 3D space actually hides part of the truth. Transforming the plane of rotation into an axis loses some information about its semantics, which causes problems for example when you want to transform the rotation itself (ex: the idea of an axial vector in 3D is a hack). But you can’t even transform the plane into an axis in any dimensions but three, so considering the general case helps us avoid making this mistake.
When trying to generalize a concept we often find that some parts of the representation do not generalize at all. Then, we search for a new way to think about things, a new viewpoint that allows us to throw away the parts that don’t generalize. What we are left with is often much more beautiful than what we started with originally, because it describes the same concept, but in a much more concise and precise way.
We can use n-dimensional space as a way to discard viewpoints that are not as fundamental as others because they do not generalize.

In Miegakure, the player’s main action is a rotation (when the space appears to deform, the player is actually just turning their head 90 degrees into the fourth dimension) and there are rotating objects in the game. So the player is learning about rotation in a more general context and it enlightens their concept of rotation in 3D.
I think this idea of distilling and generalizing concepts happens in other games, in some form.

Frank Lantz talked about similar ideas in this great talk.
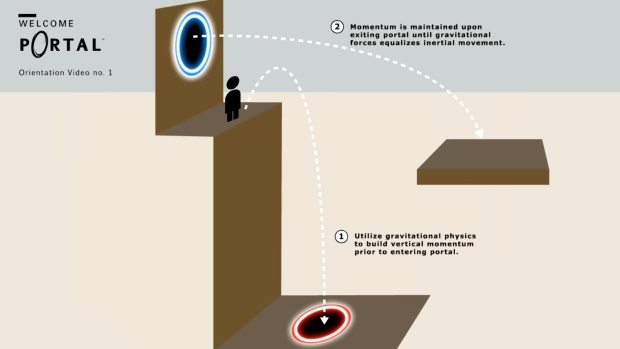
Portal takes the usual laws of physics and adds portals to them. There’s some exploration of what having portals might mean by themselves, but what is especially interesting to me is the way that Portals affect things like momentum.
The idea of using gravity to increase momentum then rotating that momentum to cross a pit makes the player think about momentum in a different way and that reveals things about it. Momentum is seen through the more general lens of portals. There are actually problems with this because it is difficult to cleanly generalize, but I will talk about it more next time.